Estrategia diseñada y aportada por: Karen Citlaly Rugerio Gómez.
A lo largo de nuestra formación y desempeño profesional, no hemos sido pocos los que hemos escuchado y advertido que, de alguna manera, casi misteriosa pero explicable hasta cierto punto, a una gran parte de nuestros alumnos (docentes también desde luego) no les gustan o no les agradan las matemáticas. Es de conocimiento público que para mucha gente esta materia suele ser más que un reto…hasta tabú para muchos otros más. Y sin embargo, es imposible vivir sin convivir con los números. Dominan cada momento de nuestra existencia y sin duda son artífices del avance constante de la humanidad.
Muchos le tuvimos temor a las matemáticas ya sea porque tuvimos maestros poco comprometidos, otros porque nuestros padres nos enseñaron a su manera y modo y en un momento dado hubo un choque con lo que íbamos aprendiendo en la escuela, algunos más nos acercamos de manera intuitiva o autodidacta y no menos representan el bloque de quienes les apasionan y divierten los números no como conceptos abstractos, sino como lo más natural y lógicamente coherente en el universo.
[quads id=1]
Nuestros planes y programas también han sufrido esa vorágine pues pasamos de sistemas de enseñanza basados en el aprendizaje memorístico de números u operaciones sin una conexión lógica a modelos inspirados en la reflexión y análisis más allá de lo que hemos conocido como la aritmética. Vivimos una encarnizada lucha entre quienes decían que fuéramos “hábiles” en el calculo mental, por citar un ejemplo, y quienes decían que no importaba lo que tardáramos, si encontrábamos la respuesta correcta, ya nos podíamos dar por bien servidos. Otra lucha había cuando nos pedían explicar “el procedimiento” por el cuál encontramos nuestras respuestas. Si atinábamos al del docente, ya teníamos un punto adicional, si no era así, éramos mecedores de taches y llamadas de atención porque “no era posible” encontrar una respuesta sin escribir un procedimiento.
Mucha de esta polémica sigue estando viva y es evidente que en el corto plazo no podremos dar por ganador a unas u otras posturas metodológicas, pues al final del día tenemos una guía curricular que, acorde a los tiempos modernos, no se basa exclusivamente en la memoria o el razonamiento por sí mismos o aisladamente trabajando uno con otro, sino que parte del concepto del aprendizaje situado.
Sirve recordar lo que dice el marco curricular. De acuerdo con el Plan de estudios 2011 “los avances logrados en el campo de la didáctica de la matemática en los últimos años dan cuenta del papel determinante que desempeña el medio, entendido como la situación o las situaciones problemáticas que hacen pertinente el uso de las herramientas matemáticas (…) así como los procesos que siguen los alumnos para construir conocimientos” (SEP. Programas de estudio. Guía para el maestro 3er grado. 2011)
[quads id=1]
Por su parte, el Plan 2017 conocido también como de Aprendizajes clave para la educación integral, considera que “las matemáticas son un conjunto de conceptos, métodos y técnicas mediante los cuales es posible analizar fenómenos y situaciones en contextos diversos (…) así, comprender sus conceptos fundamentales, usar y dominar sus técnicas y métodos y desarrollar habilidades matemáticas (…) tiene el propósito de que los estudiantes identifique, planteen y resuelvan problemas, estudien fenómenos y analicen situaciones y modelos en una variedad de contextos” (SEP. Aprendizajes clave para la educación integral. 1er grado. 2017)
Nótese como ambos marcos curriculares conciben a las matemáticas (y más específicamente el pensamiento matemático) como un algo en constante crecimiento y desarrollo, no meramente memorístico o abstracto y que como docentes debemos ayudar a desarrollar en cada uno de nuestros alumnos no forzando etapas del pensamiento.
En la zona escolar 019, la compañera Karen Citlaly Rugerio Gómez ha desarrollado con sus alumnos una estrategia novedosa denominada “Algoritmos alternativos”, la cual fue incluso tema de un programa de Aprende en Casa edición Tlaxcala (puede verse en la siguiente liga: https://youtu.be/9bmEO7WQ11A). A continuación, la maestra Karen nos explica su trabajo.
[quads id=1]
“¿Qué es un algoritmo?… dice Fernández (2005), “se identifica en el conjunto de una secuencia de pasos operativos para la realización de una tarea o la resolución de un problema” (p. 32). Si bien esta definición resulta sencilla, podemos encontrar otras que completan su significado: … serie finita de reglas a aplicar en un orden determinado a un número finito de datos para llegar con certeza (es decir, sin indeterminación ni ambigüedades), en un número finito de etapas, a cierto resultado, y esto, independientemente a los datos. (Buendía, Fernández y Rico, 1990, p. 51) … sucesión finita de reglas elementales, regidas por una prescripción precisa y uniforme, que permite efectuar paso a paso, en un encadenamiento estricto y riguroso, ciertas operaciones de tipo ejecutable, con vistas a una resolución de los problemas pertenecientes a una misma clase (Gallardo, 2004). Para Ñabraña (2002) un algoritmo permite obtener resultados sin tener que justificar los pasos dados; exige rigor, orden, concentración y práctica; puede ser popularizado ya que no es necesario comprender por qué funciona, basta con saber cómo funciona.
Desde un punto de vista matemático un algoritmo es un método sistemático que te ayuda a resolver operaciones numéricas, y a su vez consta de un conjunto finito de pasos guiados por unas reglas que nos facilitan el cálculo, según el punto de vista, y llegar a un resultado exacto.
Ventajas de algoritmos alternativos
Atendiendo a las necesidades de un cambio no solo curricular si no de pensamiento, a lo largo de los años, lo que ha traído consigo causa que según Pérez (2005) basa en:
- Cuestionamiento de otros algoritmos en los currículums.
- Renovación pedagógica de los 50 con inspiración constructivista.
- Uso social en el que cada vez menos se hacen cuentas con lápiz y papel.
- Movimientos a favor de la abolición de los algoritmos tradicionales que piden más estrategias para cálculo mental y uso de la tecnología: calculadora)
[quads id=1]
Es preciso destacar que “Es bueno que los niños conozcan más de un algoritmo para una misma operación, de modo que puedan elegir según las cantidades implicadas, el tiempo disponible, etc.” (Bermejo et al., 2009). De esta manera los estudiantes pueden realizar conexiones a partir de vida cotidiana o su contexto a diferencia del algoritmo tradicional.
Desde el punto de vista de diferentes autores las ventajas más significativas de conocer desarrollar o aprender un algoritmo alternativo son:
- Cálculo mental (Iglesias, 2005; Martínez, 2001).
- Estimación (Martínez, 2001).
- Uso y construcción de materiales (Meavilla y Oller, 2014).
- Procedimientos personales: aproximación por redondeo, búsqueda de puntos de referencia por exceso y defecto, descomposiciones, intuición de proporcionalidad (Fernández, 2005; Iglesias, 2005; Meavilla y Oller, 2014).
Todas las ventajas que se desarrollan anteriormente tienen un sentido de pertenencia e identificación con la finalidad de conocer las operaciones básicas y no solo conocer el algoritmo que las define.
Sustracción
La sustracción: La resta no es una operación independiente. Para saber restar es necesario saber sumar. La operación de restar se estudia principalmente, en la educación primaria, como sustracción y como complementariedad la representación matemática de esta operación como sustracción no es fácil para el niño, debido a que el sustraendo se representa como cantidad distinta, sin serlo.
Esto nos lleva a una descripción, no solo a partir de una definición de la sustracción, también atenderlo desde una reflexión de su propósito y el manejo que el estudiante le puede dar al algoritmo de sustracción, es preciso identificar el uso de esta operación en el ámbito escolar, así como en la vida cotidiana. Esto es, ir más allá de saber resolver el algoritmo de una forma mecánica, y en cambio alcanzar a entender el sentido de cada uno, para poder aplicarlo en problemas de la vida cotidiana de una manera efectiva.
[quads id=1]
De esta manera defino “resta por eliminación de valor común” como un algoritmo alternativo (diferente al algoritmo tradicional establecido), aplicado posterior a la metodología de las regletas Cuisenaire, como se explica a continuación:
Metodología de la sustracción por eliminación de valor común.
- Tener una operación de sustracción.
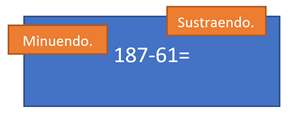
- Identificar cada uno de los elementos o partes que integran una sustracción

- Identificar los valores del sustraendo

- Descomponer el sustraendo

- Descomponer minuendo de tal manera que estén presentes los números que integran el sustraendo
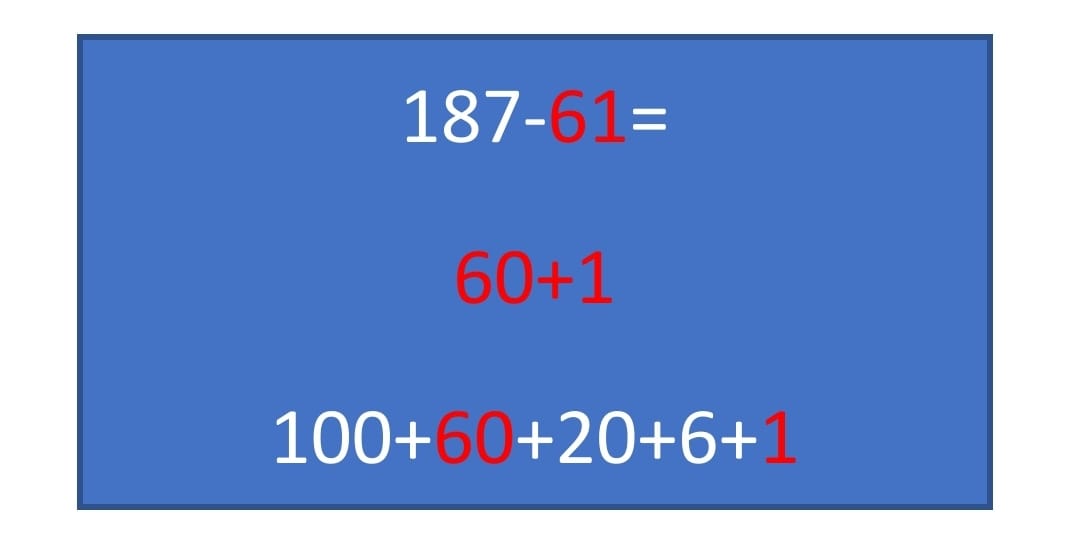
- Eliminar los valores comunes del sustraendo que se encuentren en el minuendo.

- Sumar los valores del minuendo restando
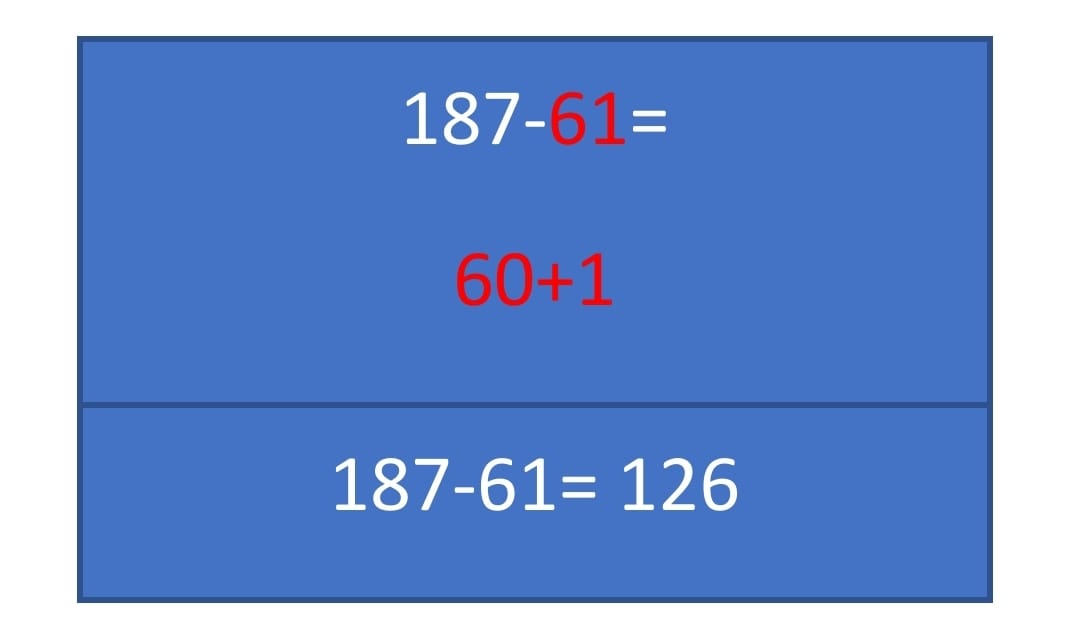
Bibliografía
Buendía Eisman, L.; Fernández Cano, A. y Rico Romero, L. (1990). Algoritmos y estrategias en la enseñanza del cálculo básico. Revista de investigación educativa, RIE, 8(15), 51-62.
Fernández Bravo, J.A. (2005). Avatares y estereotipos sobre la enseñanza de los algoritmos en matemáticas. Unión: revista iberoamericana de educación matemática, 4, 31-46.
Gallardo Romero, J. (2004). Diagnóstico y evaluación de la comprensión del conocimiento matemático. El caso del algoritmo estándar escrito para la multiplicación de números naturales (Tesis Doctoral no publicada). Málaga: Departamento de Didáctica de la Matemática, de las Ciencias Sociales y de las Ciencias Experimentales, Universidad de Málaga.
Iglesias Pérez, J.M. (2005). Los algoritmos tradicionales y otros algoritmos. Unión: revista iberoamericana de educación matemática, 4, 47-49.
Martínez Montero, J. (2001). Los efectos no deseados (y devastadores) de los métodos tradicionales de aprendizaje de la numeración y de los algoritmos de las cuatro operaciones básicas. Epsilon: Revista de la Sociedad Andaluza de Educación Matemática “Thales”, 49, 13-26.
Meavilla Seguí, M. y Oller Marcén , A.M. (2014). Gaspar de Texeda y los algoritmos de la multiplicación. Suma: Revista sobre Enseñanza y Aprendizaje de las Matemáticas, 75, 61-73.
Ñabraña, A. (2002). Algoritmos e Matemáticas. Eduga: revista galega do ensino, 34, 147-166.
Pérez, A.J. (2005). Algoritmos en la enseñanza y el aprendizaje de las matemáticas. Unión: revista iberoamericana de educación matemática, 1, 37-44.
Roa Guzmán, R. (2007). Algoritmos de cálculo. En Castro Martínez, E. (Ed.), Didáctica de la matemática en la Educación Primaria (pp. 231-256). Madrid: síntesis.





